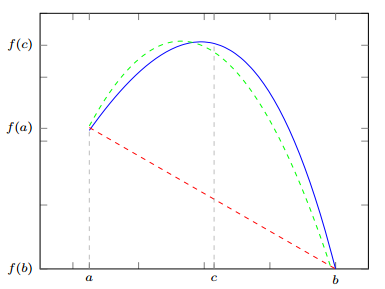
Integral \(f(x)\) dengan batas \([a,b]\) menggunakan metode simpson adalah melakukan integral dengan interpolasi kuadrat terhadap \(f(x)\). Oleh karena interpolasi orde dua membutuhkan tiga titik maka banyak partisi metode simpson harus genap. Interval \([a,b]\) yang dipartisi dua bagian menjadi tiga titik, yaitu
$$x_0=a,\quad x_1=a+h,\quad x_2=b$$
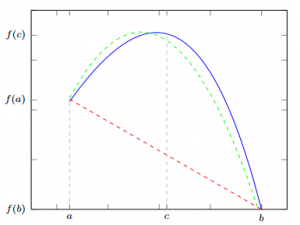
Interpolasi orde dua terhadap fungsi \(f(x)\) pada titik-titik \(\{x_0,x_1,x_2\}\) adalah
$$ P_2(x)=L_0y_0+L_1y_1+L_2y_2 $$
dengan \(L_0=\dfrac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}\), \(L_1=\dfrac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}\), dan \(L_2=\dfrac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}\).
Integral \(P_2(x)\) dengan batas \([a,b]\) menghasilkan
$$S_2=\dfrac{b-a}{3}\left(f_0+4f_1+f_2\right)$$
Jika interval \([x_0,x_1]\) dan \([x_1,x_2]\) masing-masing di partisi dua agar dapat diinterpolasi lagi dengan orde dua, maka terdapat empat interval, yaitu
$$[a,b]=[x_0,x_1] \cup [x_1,x_2] \cup [x_2,x_3] \cup [x_3,x_4]$$
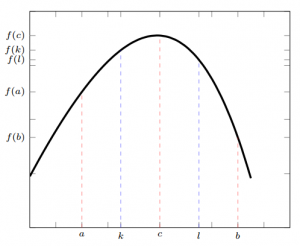
Integral dilakukan di partisi \(\{x_0,x_1,x_2\}\) dan \(\{x_2,x_3,x_4\}\) dengan integral per partisinya adalah
$$S_2^i=\dfrac{h}{3}\left(f_{i}+4f_{i+1}+f_{i+2}\right)$$
untuk i=0,2, atau
$$S_4=\dfrac{h}{3}\left(f_{0}+4f_{1}+2f_{2}+4f_{3}+f_{4}\right)$$
Secara umum, integral numerik fungsi \(f(x)\) menggunakan metode Simpson adalah
$$S_n=f(x_0)+f(x_n)+4\sum_{i=0}^{n/2}{f(x_{2i+1})}+2\sum_{i=1}^{n/2-1}{f(x_{2i})}$$
dengan \(n\) adalah banyak partisi genap pada interval \([a,b]\).
Komputasi dengan python
Import modul numpy untuk keperluan array
import numpy as np
Buatlah procedure untuk menghitung fungsi
f=lambda x:np.sin(x)+np.cos(x)
Buatlah procedure simpson dengan input fungsi, batas bawah a, batas atas b dan banyak partisi, n.
def simpson(f,a,b,n): h=(b-a)/n x=np.linspace(a,b,n+1) fx=f(x) fgan=fx[1:n:2] fgen=fx[2:n:2] hasil=fx[0]+fx[n]+4*np.sum(fgan)+2*np.sum(fgen) hasil=hasil*h/3 return hasil
Hasil simulasi ditunjukkan pada Tabel
| \(n\) | \(S_n\) |
| 10 | 2.325465 |
| 100 | 2.325444 |
| 1000 | 2.325444 |
| 10000 | 2.325444 |