Integral tentu dari fungsi \(f(x)\) pada batas [a,b] dinyatakan dengan
$$I=\int_{a}^{b}{f(x) \;dx}$$
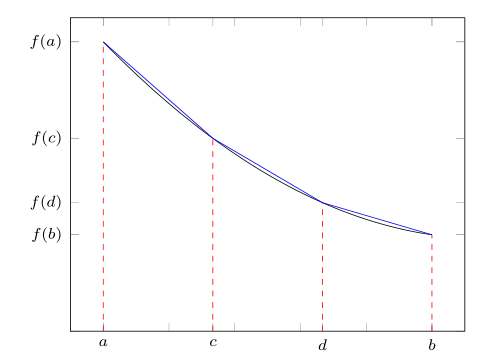
Jika \(f(x)\) adalah fungsi yang sulit diintegralkan atau tidak diketahui anti-derivatifnya, ya digunakan integral numerik. Misalkan \(P_1\) adalah hampiran linier bagi fungsi \(f(x)\), perhatikan Gambar 1.
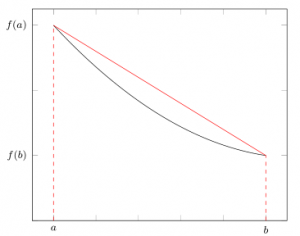
$$I\approx \int_{a}^{b}{P_1(x) \;dx}$$
Nilai integral di ruas kanan adalah luasan trapesium dengan panjang alas \(h=(b-a)\) dan tinggi kedua sisi adalah \(f(a)\) dan \(f(b)\). Jadi, didapatkan
$$\int_{a}^{b}{P_1(x) \;dx}=\dfrac{b-a}{2}(f(a)+f(b))$$
Jika pada interval \([a,b]\) dilakukan beberapa partisi, perhatikan Gambar 2.
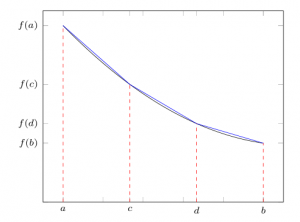
Integral fungsi \(f(x)\) dapat dihitung dari hampiran masing-masing partisi, atau
$$\int_{a}^{b}{f(x) \;dx}\approx \int_{a}^{c}{P_1(x) \;dx}+\int_{c}^{d}{P_1(x) \;dx}+\int_{d}^{b}{P_1(x) \;dx} $$
Akibatnya, diperoleh
$$\int_{a}^{b}{f(x) \;dx}\approx \dfrac{c-a}{2}(f(a)+f(c))+\dfrac{d-c}{2}(f(c)+f(d))+\dfrac{b-d}{2}(f(d)+f(c))$$
Jika lebar tiap partisi dibuat sama, atau \(c-a=d-c=b-d\), maka lebar tiap partisi adalah
$$h=\dfrac{b-a}{3}$$
Secara umum, integral numerik menggunakan metode Trapesium, untuk fungsi \(f(x)\) pada batas \([a,b]\) dengan banyak partisi \(n\) adalah
$$I=f(x_0)+f(x_n)+2\sum_{i=1}^{n-1}{f(x_i)}$$
dengan \(x_0=a,x_n=b\) dan \(x_i=x_0+hi\) untuk \(i=1,2,\ldots,n-1\).
Komputasi dengan Python
Untuk komputasi dengan python, hanya membutuhkan satu modul, yaitu numpy. Jadi, langkah pertama adalah mengimport modul numpy.
import numpy as np
Kedua adalah membuat procedure untuk fungsi yang diintegralkan. Inputnya adalah domain fungsi
def f(x): return x**2-6*x+8
Berikutnya adalah membuat procedure untuk metode trapesium. Inputnya adalah fungsi, batas integral dan banyak partisi.
def trap(a,b,n,f):
x=np.linspace(a,b,n+1)
h=np.diff(x)[0]
nf=f(x)
trap=nf[0]+nf[n]+2*np.sum(nf[1:n])
trap=0.5*h*(trap)
return trap
Selanjutnya adalah melakukan tes. Misalkan untuk fungsi \(f(x)=x^2-6x+8\) pada batas \([0,2]\) yang integral analitiknya adalah \(20/3\). Hasil untuk beberapa partisi \(n=1,10,100,1000,10000\) ditunjukkan pada Tabel.
| n | integral | eror |
| 1 | 8.00000000 | 1.33333333 |
| 2 | 6.68000000 | 0.01333333 |
| 3 | 6.66680000 | 0.00013333 |
| 4 | 6.66666800 | 0.00000133 |
| 5 | 6.66666668 | 0.00000001 |