Diberikan fungsi \(f(x)\). Pilih satu titik, misalkan \(x_0\), sehingga didapatkan pasangan titik \((x_0,f(x_0))\). Pada titik \(x=x_0\) dibuat garis singgung, dengan kemiringan \(f'(x_0)\). Garis lurus yang melewati titik \(x_0\) dengan kemiringan \(f(x_0)\) adalah
$$y-f(x_0)=f'(x_0)(x-x_0)$$
Misalkan garis lurus \(y(x)\) memotong sumbu-x di titik \(x=x_1\), dimana \(y(x_1)=0\), akan diperoleh
$$x_1=x_0-f(x_0)/f'(x_0)$$
Jadi, sekarang diperoleh titik \((x_1,f(x_1))\).
Pada titik \((x_1,f(x_1))\) dibuat garis singgung. Kemiringan pada titik ini adalah \(f'(x_1)\). Garis lurus yang melewati titik \(x_1\) dengan kemiringan \(f'(x_1)\) adalah
$$y-f(x_1)=f'(x_1)(x-x_1)$$
Misalkan garis lurus \(y(x)\) memotong sumbu-x di \(x=x_2\), dimana \(y(x_2)=0\), maka diperoleh
$$x_2=x_1-f(x_1)/f'(x_1)$$
Jika proses ini diteruskan, maka diperoleh bentuk umum,
$$x_n+1=x_n-f(x_n)/f'(x_n)$$
dengan \(n=0,1,2,N-1\) dan \(x_0\) adalah tebakan awal.
Komputasi dengan python
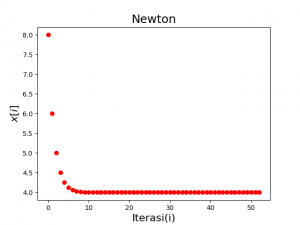
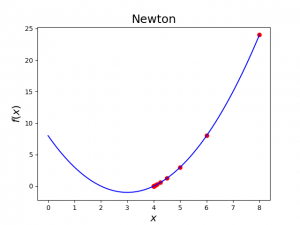
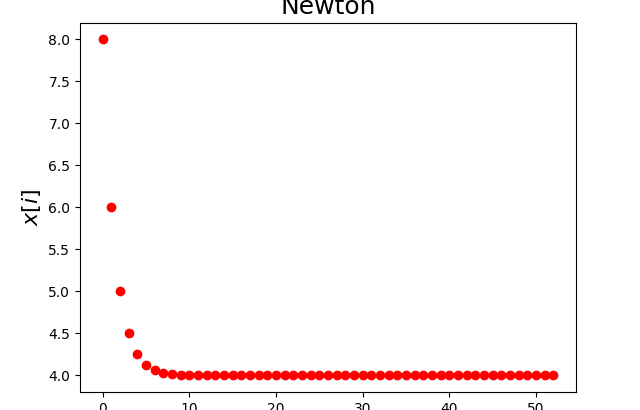
Diberikan fungsi \(f(x)=x^2-6x+8\) yang akarnya adalah \(\{2,4\}\). Akan ditentukan akarnya menggunakan metode Newton dengan tebakan awal \(x_0=8\). Untuk bekerja dengan python, 2 modul dianggap cukup. (1) modul numpy digunakan untuk bekerja dengan array dan (2) matplotlib digunakan untuk visualisasi. Jika proses visualisasi dianggap tidak diperlukan, modul ini bisa tidak diikutsertakan.
import numpy as np import matplotlib.pyplot as plt
Buat procedure untuk fungsi \(f(x)\)
def f(x): return x**2-6*x+8
Buat procedure untuk turunan fungsi \(f'(x)\)
def df(x): return 2*x-6
Buat procedure untuk metode Newton. Metode Newton membutuhkan input fungsi \(f(x)\), turunan fungsi \(f'(x)\) tebakan awal \(x_0\), toleransi eror maksimum (tolmax), jumlah iterasi maksimum (itmax).
def newton(f,init,tolmax,itmax):
x=np.zeros(itmax)
x[0]=init
for i in range(itmax-1):
x[i+1]=x[i]-f(x[i])/df(x[i])
if np.abs(f(x[i+1]))<tolmax
break
return i,x[i+1],f(x[i+1])
Hasil ditampilkan pada Gambar 1 dan 2.