Diberikan fungsi \(f(x)\). Pilih dua titik sehingga terdapat dua pasang pasangan titik, yaitu \((x_0,f_0)\) dan \((x_1,f_1)\). Garis lurus yang melalui dua titik diberikan oleh
$$(y-f_1)/(f_0-f_1)=(x-x_1)/(x_0-x_1)$$
Garis lurus ini memotong sumbu-x, misalkan di \(x=x_2\), sehingga \(f(x_2)=0\). Jadi, diperoleh
$$x_2=x_1-f_1(x_1-x_0)/(f_1-f_0)$$
Sekarang, terdapat dua pasang pasangan titik \((x_1,f_1)\) dan \((x_2,f_2)\). Garis lurus yang melalui dua titik ini adalah
$$(y-f_2)/(f_1-f_2)=(x-x_2)/(x_1-x_2)$$
Saat garis lurus memotong sumbu-x, misalkan \(x=x_3\), berlaku \(f(x_3)=0\) dan
$$x_3=x_2-f(x_2)(x_1-x_2)/(f(x_1)-f(x_2))$$
Terdapat pola yang sama untuk dua langkah yang sudah dilakukan. Secara umum, untuk \(i=1,2,\ldots,N\) diperoleh
$$x_{n+1}=x_{n}-f(x_{n})\dfrac{(x_{n}-x_{n-1})}{(f(x_n)-f(x_{n-1}))}$$
dengan \(x_0,x_1\) tebakan awal yang dipilih.
Komputasi dengan python
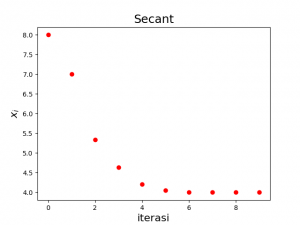
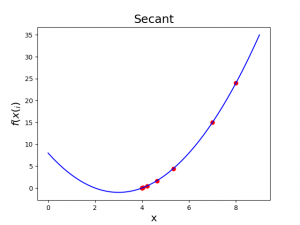
Diberikan fungsi \(f(x)=x^2-6x+8\) yang akar analitiknya \(\{2,4\}\). Akan ditentukan akar secara numerik menggunakan metode Secant, dengan tebakan awal \(x_0=8\) dan \(x_1=7\).
Pertama, import modul yang digunakan. Modul untuk proses numerik biasanya numpy dan untuk visualisasi adalah matplotlib
import numpy as np import matplotlib.pyplot as plt
Buat procedure untuk evaluasi fungsi.
f=lambda x:x**2-6*x+8 itmax=100 tolmax=1e-20
Buat procedure untuk metode Secant. Procedure secant memiliki beberapa input yaitu tebakan awal x0 dan x1, fungsi f, iterasi maksimum, dan toleransi maksimum.
x=np.zeros(itmax)
x[0]=8;
x[1]=7;
# perulangan
for i in range(1,itmax):
x[i+1]=x[i]-f(x[i])*(x[i]-x[i-1])/(f(x[i])-f(x[i-1]))
print('%2d' % i,\
'%.15f' % x[i],\
'%.5e' % f(x[i]))
if np.abs(f(x[i+1]))<tolmax:
break
Hasil simulasi ditunjukkan pada Gambar 1 dan 2.