Diberikan fungsi \(f(x)\) yang terdefinisi pada \(I=[a,b]\). Pada interval ini terdapat \(\alpha\in I\) yang memenuhi $$f(\alpha)=0.$$
Tanpa mengurangi keumuman, dimisalkan bahwa \(f(x)<0\) yang berlaku untuk \(x\in[a,\alpha]\) dan \(f(x)>0\) yang berlaku untuk \(x\in[\alpha,b]\).
Nilai \(\alpha\) dapat ditentukan dengan mengambil titik tengah dari interval dan sub-interval \([a,b]\) yang dilakukan secara iteratif. Untuk langkah pertama, titik tengah interval \([a_1,b_1]\) adalah $$c_1=\dfrac{a_1+b_1}{2}.$$
Perlu ditentukan subinterval baru, apakah \([a_1,c_1]\) atau \([c_1,b_1]\). Jika nilai \(c_1\) mengakibatkan \(f(c_1)<0\) maka nilai \(c_1\) lebih mendekati \(\alpha\) dibandingkan \(a_1\). Sebaliknya, jika nilai \(c_1\) mengakibatkan \(f(c_1)>0\) maka nilai \(c_1\) lebih mendekati \(\alpha\) dibandingkan \(b_1\). Tanpa mengurangi keumuman, misalkan nilai \(c_1\) mengakibatkan \(f(c_1)<0\). Maka, subinterval yang digunakan adalah \([c_1,b_1]\). Atau, dapat dituliskan dengan \([a_2,b_2]\) dengan \(a_2=c_1\) dan \(b_2=b_1\).
Iterasi kedua menggunakan interval \([a_2,b_2]\). Titik tengah interval ini adalah $$c_2=\dfrac{a_2+b_2}{2}.$$
Misalkan nilai \(c_2\) mengakibatkan \(f(c_2)<0\), sama seperti analogi iterasi pertama, \(c_2\) lebih mendekati \(\alpha\) dibandingkan \(a_2\). Lalu, subinterval yang dihasilkan pada iterasi kedua adalah \([c_2,b_2]\). Atau, dapat dituliskan dengan \([a_3,b_3]\) dengan \(a_3=c_2\) dan \(b_3=b_2\).
Iterasi ketiga menggunakan interval \([a_3,b_3]\). Titik tengah interval ini adalah $$c_3=\dfrac{a_3+b_3}{2}.$$
Misalkan nilai \(c_3\) mengakibatkan \(f(c_3)<0\), sama seperti analogi iterasi pertama dan kedua, \(c_3\) lebih mendekati \(\alpha\) dibandingkan \(a_3\). Lalu, subinterval yang dihasilkan pada iterasi ketiga adalah \([c_4,b_4]\). Atau, dapat dituliskan dengan \([a_4,b_4]\) dengan \(a_4=c_3\) dan \(b_4=b_3=b_2\).
Secara umum, untuk \(i=1,2,3,\ldots,n\), digunakan interval \([a_i,b_i]\). Titik tengah interval \([a_i,b_i]\) adalah $$c_i=\dfrac{a_i+b_i}{i}.$$.
- Jika nilai \(c_i\) mengakibatkan \(f(c_i)<0\), maka \(c_i\) lebih mendekati \(\alpha\) dibandingkan \(a_i\). Interval yang digunakan selanjutnya adalah \([c_i,b_i]\)
- Jika nilai \(c_i\) mengakibatkan \(f(c_i)>0\), maka \(c_i\) lebih mendekati \(\alpha\) dibandingkan \(b_i\). Interval yang digunakan selanjutnya adalah \([a_i,c_i]\)
Perhitungan dengan python
Pertama, load modul yang digunakan, pengaturan eror dan toleransi maksimum dalam iterasi.
import numpy as np from matplotlib import pyplot as plt tolmax = 1e-20; itmax=100;
Kedua, buat procedure untuk fungsi yang akan ditentukan solusinya. Misalkan \(y(x)=x^2-5x+6\) yang solusi analitiknya adalah \(x=\{2,3\}\)
def fx(x): return x**2-5*x+6
Terakhir, procedure untuk metode Bisection
def bisection(a,b,f):
if f(a)*f(b)>0:
exit()
else:
for i in range(0,itmax):
c=0.5*(a+b)
if (f(b)*f(c))<0:
a=c
b=b
else:
a=a
b=c
if (abs(f(c))<tolmax):
break
return i,c
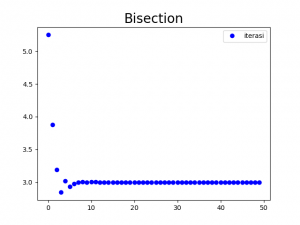
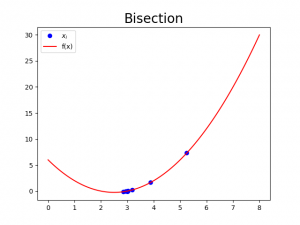
Jika dipilih tebakan awal \(a=2.5,b=8\), dinamika nilai \(c_i\) ditunjukkan pada Gambar 1. Perbandingan antara dinamika \(c_i\) dengan fungsi \(f(x)\) ditunjukkan pada Gambar 2.