Pemodelan
Misalkan \(N\) adalah jumlah populasi pada wilayah \(\Omega\). Diasumsikan wilayah \(\Omega\) adalah wilayah tertutup. Akibatnya,
- tidak ada penduduk masuk dan keluar
- Dinamika penduduk hanya bergantung pada kelahiran dan kematian.
- Besarnya jumlah kelahiran dan kematian sebanding dengan jumlah populasi saat itu.
Banyak kelahiran diasumsikan proporsional terhadap jumlah populasi di interval waktu pengamatan
$$\Delta B=\beta N \Delta t$$
Banyak kematian pada waktu pengamatan adalah proporsional terhadap jumlah populasi di interval waktu pengamatan
$$\Delta D=\delta N \Delta t$$
Perubahan jumlah penduduk pada masa pengamatan adalah
$$\Delta N=\Delta B – \Delta D=(\beta-\delta) N \Delta t$$
Perubahan tiap satuan waktu menjadi
$$\dfrac{\Delta N}{\Delta t}=\Delta B – \Delta D=(\beta-\delta) N $$
Untuk \(\Delta t\to 0\) menghasilkan
$$\dfrac{dN}{dt}=\gamma N(t)$$
dengan \(\gamma=\beta-\delta\). Jika jumlah kelahiran lebih besar, maka \(\gamma\) bernilai positif. Sebaliknya, nilai \(\gamma\) bernilai negatif.
Solusi analitik
Nyatakan persamaan dinamik dalam bentuk
$$\dfrac{dN}{N}=\gamma d(t)$$
Integral masing-masing ruas untuk \(t\geq0\) menghasilkan
$$\int_{0}^{t}{\dfrac{dN(\tau)}{N(\tau)}}=\int_{0}^{t}{\gamma d(\tau)}$$
Hasil integral di ruas kiri dan kanan adalah
$$\ln(N(t))-\ln(N(0))=\gamma t$$
Menggunakan aturan logaritma
$$\ln\left(\dfrac{N(t)}{N(0)}\right)=\gamma t$$
Hitung eksponen di masing-masing ruas,
$$N(t)=N(0)\exp(\gamma t)$$
dengan \(N(0)\) adalah jumlah populasi awal atau \(N(t=0)\)
Penentuan Parameter dari Data
Diberikan \(n\) pasang data \((t_i,d_i)\) untuk \(i=1,2,\ldots,n\). Akan ditentukan \(\gamma\) yang membuat model eksponensial mengikuti pola data yang diberikan. Kita definisikan kata mengikuti pola dengan eror antara data dan model minimum.
Didefinisikan eror data dan model
$$e=\dfrac{1}{2}\sum_{i=1}^{n}{\left[\ln(d_i)-\ln(N_i)\right]^2}$$
dengan \(N_i=N(t_i)\). Penggunaan logaritma bertujuan agar fungsi eksponensial menjadi fungsi polinom linier. Hal ini untuk menghindari metode iterasi dalam menentukan parameter optimal fungsi taklinier. Substitusikan fungsi N menghasilkan
$$e=\dfrac{1}{2}\sum_{i=1}^{n}{\left[\ln(d_i)-\ln(N_0)-\gamma t_i \right]^2}$$
Untuk meminimumkan \(e\), ditentukan nilai \(\gamma\) yang bersesuaian. Turunan \(e\) terhadap \(\gamma\) menghasilkan
$$\partial e/\partial \gamma=\sum_{i=1}^{n}{\left[\ln(d_i)-\ln(N_0)-\gamma t_i \right]t_i}$$
Karena \(\partial e/\partial \gamma=0\) adalah titik kritis dan menggunakan aturan logaritma, maka diperoleh
$$\sum_{i=1}^{n}{\ln(d_i/N_0)t_i}=\gamma\sum_{i=1}^{n}{\gamma t_i^2}$$
Jadi, nilai \(\gamma\) yang memenuhi adalah
$$\gamma=\dfrac{\sum\limits_{i=1}^{n}{t_i\ln(d_i/N_0)}}{\sum\limits_{i=1}^{n}{ t_i^2}}$$
Turunan kedua \(e\) terhadapa \(\gamma\) menghasilkan
$$d^2e/d\gamma^2=\sum_{i=1}^{n}{- t_i^2}$$
yang selalu bernilai negatif. Akibatnya, nilai \(\gamma\) yang memenuhi \(de/d\gamma=0\) adalah titik minimum.
Simulasi
Diberikan data
| t | y |
| 0 | 4 |
| 0.25 | 6.467352 |
| 0.5 | 8.472984 |
| 0.6 | 9.468 |
| 0.75 | 12.21436 |
| 0.9 | 17.32087 |
| 1 | 15.96137 |
| 1.2 | 18.92676 |
| 1.45 | 27.50297 |
| 1.5 | 31.08328 |
| 1.6 | 34.55622 |
| 1.75 | 36.65161 |
| 1.8 | 41.95094 |
| 2 | 50.72998 |
Berdasarkan data, diperoleh
$$\begin{array}{lcl}\sum\limits_{i=1}^{20}{t_i^2}&=&21.7\\ \sum\limits_{i=1}^{20}{t_i\ln(d_i/N_0)}&=&28.9262809\end{array}$$
Nilai \(\lambda\) yang memenuhi adalah
$$\lambda=\dfrac{28.9262809}{21.7}=1.333008336$$
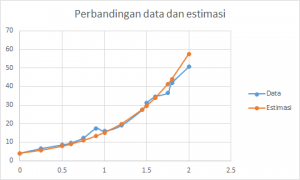
Perbandingan antara data dan kurva estimasi ditunjukkan pada Gambar 1.
Download data : github/kmutamar/dataKuliah